Arithmetic (Mathematic) Controller
Description
A controller whose output combines two or more input controllers using some specific arithmetical or mathematical operation.
Syntax and Default Values
The arithmetic controller can be created using the following Mlys (Max), mlys.lua, or Lisp syntax:
In Modalys for Max, this object is named mlys.arithmetic:
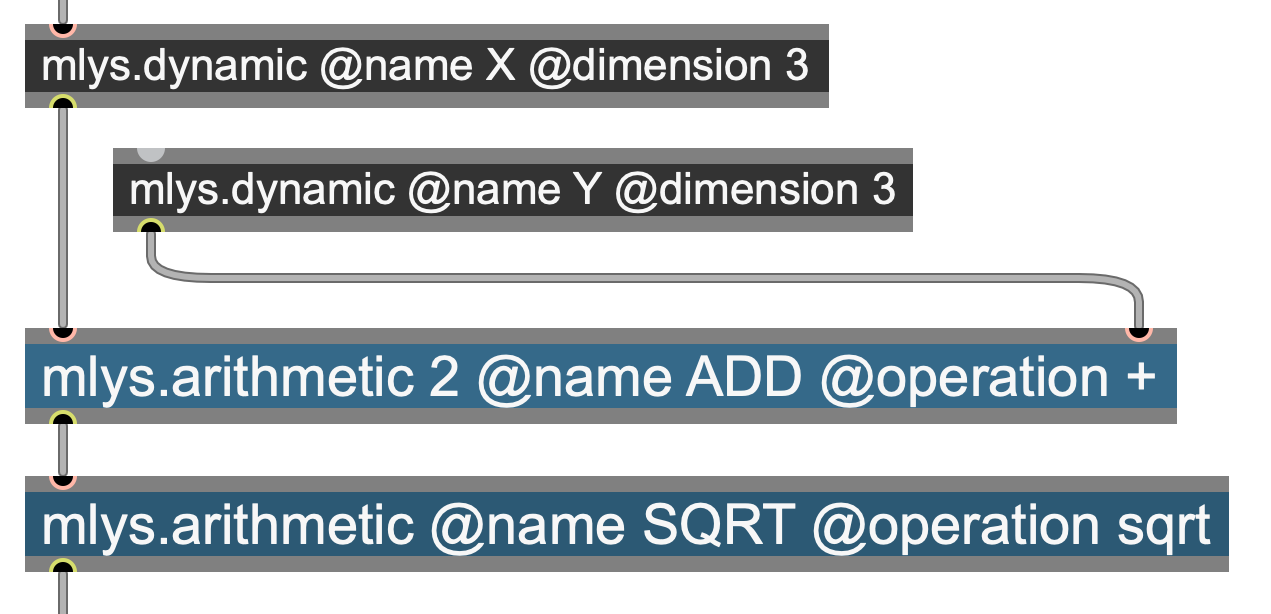
(In this example we combine an arithmetic controller with 2 inputs and another with just one input).
c1 = create_controller{kind="dynamic",value={4.5, -2.1}}
c2 = create_controller{kind="dynamic",value={3.2, -45.9}}
c3 = modalys.create_controller{kind="arithmetic",name="MyArithmetic",
operator="*",input={c1,c2}}
(make-controller 'arithmetic
dimension
operator
c1 c2 ... )
(make-controller 'arithmetic
dimension
operator
(list c1 c2 ... ))
Available Operations
Some operators take just one input (sine, sqrt, 1/x, abs, sign, etc.), some take 2 (power, mod, etc.), and others take potentially multiple inputs (addition, multiplication etc.). The golden rule is that the dimension of all input controllers must be the same. Operations are:
• addition ("+")
• substraction ("-")
• multiplication ("*")
• division ("/")
• square root ("sqrt")
• power ("^" ou "pow")
• 1/x ("inv")
• sine ("sin")
• cosine ("cos")
• tangent ("tan")
• exponential ("exp")
• log of base e ("log")
• modulo ("mod")
• absolute value ("abs")
• sign function ("sign")
• min
• max
• inferior comparator ("<")
• inferior or equal comparator ("<=")
• equal comparator ("=")
• superior or equal comparator (">=")
• superior comparator (">")
Parameters
The 'arithmetic controller takes the following arguments:
- dimension: dimension of the arithmetic controller (should be set to -1 to set the dimension of the input controllers automatically).
- operator: one of these symbols: +, -, *, /, sqrt, pow (or ^), inv (or 1/x), sin, cos, tan, exp, log, mod, abs, sign, min, max, <, <=, =, >, >= (in quotes, or preceded by an apostrophe for Lisp)
- c1, c2, etc.: controllers to feed the math operation (in Mlys, they are connected as inlets.)
The dimension of all input controllers and the resulting output controller should match.
Any number of input controllers may be provided, but they must all have the same dimension. The controllers may be provided as a series of arguments or as a list.
Discussion
Arithmetic controllers are used to realize arithmetic operations efficiently in controller networks.
A basic example shows two breakpoint envelopes being multiplied together (as shown in the image at the top of the page):
(setq c1 (make-controller 'envelope 1 '((0 0.0) (0.2 1.0) (0.4 0.7) (1.2 0.7) (2 0))))
(setq c2 (make-controller 'envelope 1 '((0 1.5) (2 0.25)) ))
(setq my-product (make-controller 'arithmetic -1 '* c1 c2))
(defun +~ (c0 c1) (make-controller 'arithmetic -1 "+" (list c0 c1)))
(defun *~ (c0 c1) (make-controller 'arithmetic -1 "*" (list c0 c1)))
(defun sin~ (frequency) (make-controller 'sine 1 frequency))
;;; we assume here that cf, mr, mi and ae are bound to one-dimensional controllers
(setq mrcf (*~ mr cf))
(setq fm-output (*~ (sin~ (+~ (*~ (*~ mrcf mi) (sin~ mrcf)) cf)) ae))
★