3D Finite Elements

Introduction

The 3D Finite Elements object allows the definition of three-dimensional objects in Modalys, using a mesh, which is then converted to modal data with the help of numerical methods. The introduction of finite elements in Modalys is the work of Joël Bensoam after his brillant PHD thesis (2003).

Although the instantiation of the 'finite-element object itself is documented within the Object Reference, this section of the documentation will eventually be expanded to include the family of functions that assist in the creation of these objects.

And last but not least, finite elements are available since v.3.6 in Modalys for Max, very tightly linked to the mlys.lua controller. So we suggest that you take a look at the growing lua Modalys examples within Max. That is a very good starting point.

Abstract Modalys is a sound synthesis software developed at Ircam for research and musical applications. This software allows one to build virtual instruments based on physical models to obtain the most entire range of expressive variations in the instrument in response to intuitive controls. An instrument, as a complex structure, is described by the mechanical/acoustical interaction of its components (strings, tubes, resonators, soundboard,...). Some new research have been done recently to extend the sound prediction to three- dimensional objects with the help of numerical methods. In particular, theoretical and nu- merical treatment of the unilateral and frictionless dynamic contact between two arbitrary elastic bodies was studied and highlighted by simulations implemented in Modalys. This manual presents the new functions dedicated to finite element objects.

(compute-modes)

Description

This function calculate the mode of vibration of a finite element object. Mind the fact that each time a finite element object is defined, modes must be calculated in order to process a sound synthesis. This implies that the creation of a finite element object must be followed by the function compute-modes. It is not the case with other objects where this computation is implicitly done by Modalys.

Syntax

(compute-modes my-finite-element-object)

Parameters

my-finite-element-object The modes of vibration will be computed for this object.

Example

Read a file (for example diapason.mesh) in order to assign a mesh to a finite element object. Give the desired parameters (see the function make-object 'finite-element. . . ) and visualize it:

(define diapason-mesh (make-mesh 'read-from-file \"diapason.mesh\"))
(define diapason-fem ( make-object 'finite-element (mesh diapason-mesh)
                                                   (modes 30)
                                                   (density 7700)
                                                   (young 2e11)
                                                   (poisson .3)
                                                   (freq-loss 0.1)
                                                   (const-loss 0.5)))
(view 'object diapason-fem)

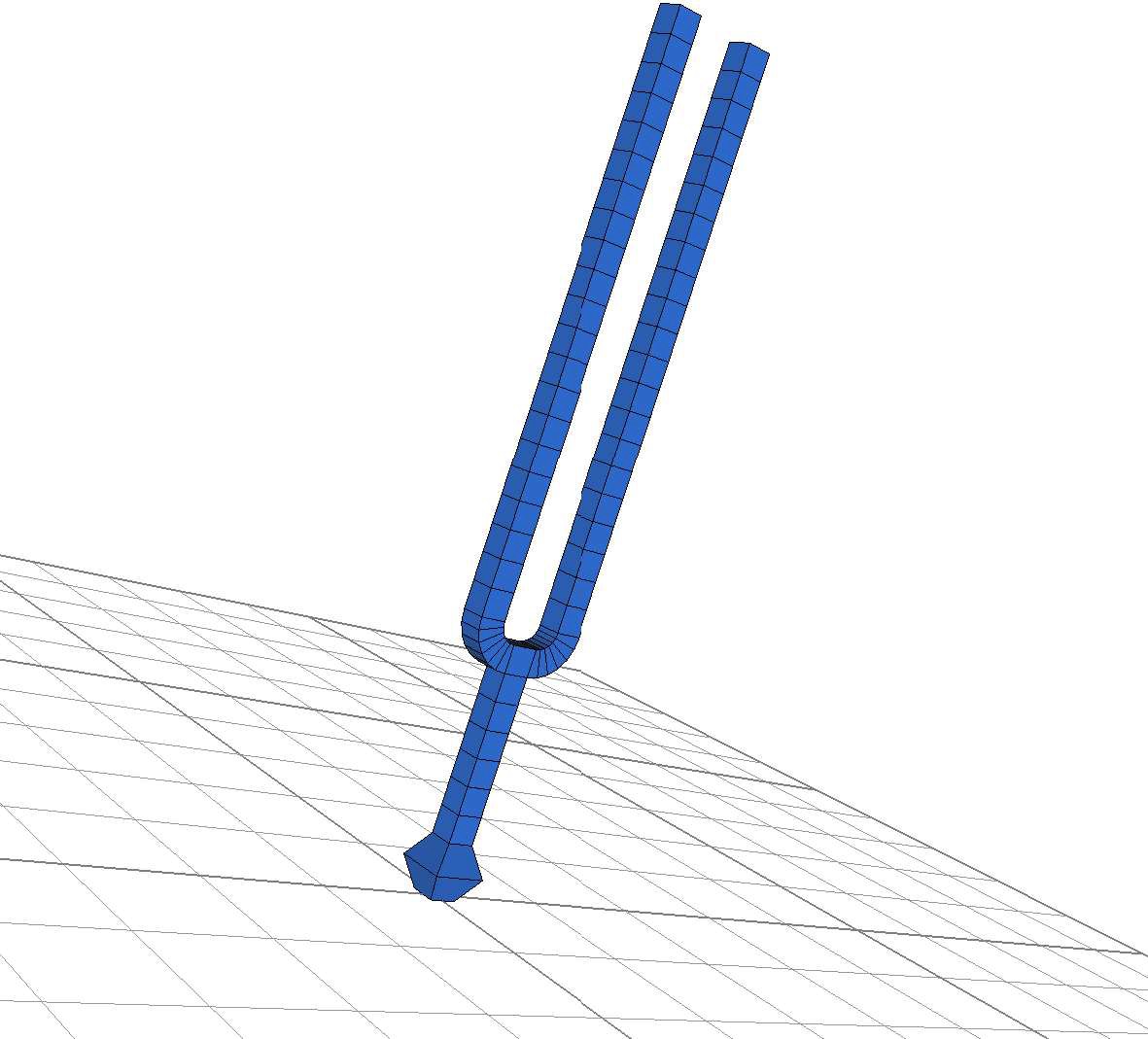
Compute the modes of vibration and visualize one of them (compute-modes diapason-fem) (view 'mode diapason-fem 18 20 5)

In the medit application right click to obtain the main-menu and choose 'Play sequence' in the 'animation' sub-menu. Use also the 'm' key.

(duplicate 'homothety)

Description

Constructs a mesh by duplication using an homothety. Points are extruded into lines, lines into quadrilaterals and quadrilaterals into hexahedras.

Syntax

(duplicate 'homothety mesh rep. homothety-point homothety-amplitude)

Parameters

mesh The mesh to be extruded by homothety. This mesh could be constituted by points, lines or quadrilaterals. rep. Number of extrusion. homothety-point Center homothety coordinates. homothety-amplitude Amplitude of the homthety

Example

Duplicate a quadrilateral into hexahedras by homothety

Define a mesh named my-mesh which contains a single quadrilateral (see duplicate 'translation for details) and visualize it:

(define my-mesh ( make-mesh 'single-point (vector 0 0 0)))
(duplicate 'translation my-mesh 1 (vector 1 0 0))
(duplicate 'translation my-mesh 1 (vector 0 0 0.5))
(view 'mesh my-mesh)

Duplicate the quadrilateral into hexahedras by an homothety (duplicate 'homothety my-mesh 2 (vector 0.5 -1 0) 1.5 ) The mesh my-mesh contains now 2 hexahedras obtained by an homothety of center (x=0.5, y=1, z=0) with an amplitude 1.5. To see the result with the homothety center, define a mesh which contains the homothety point and add it to the previous mesh (define center ( make-mesh 'single-point (vector 0.5 -1 0))) (define my-mesh (make-mesh 'add (list my-mesh center))) (view 'mesh my-mesh) In the medit application use keys 'P' and 'g'.

(duplicate 'reflection)

Description

Constructs a mesh by duplication using a reflection. Points are extruded into lines, lines into quadrilaterals and quadrilaterals into hexahedras.

Syntax

(duplicate 'reflection mesh normal invariant-point)

Parameters

mesh The mesh to be extruded by reflection. This mesh could consist of points, lines or quadrilaterals. normal The vector normal to the symetry plane. invariant-point Any point in the symetry plane.

Example

Duplicate a point into a line by reflection with the plane z = 0

;;;Define a point
(define my-mesh ( make-mesh 'single-point (vector 0 0 1)))
;;;Duplicate the point into a line by reflection
(duplicate 'reflection my-mesh (vector 0 0 1) (vector 0 0 0))
;;;The mesh my-mesh is now line of length 2 meters.
;;;To visualize the result with the symetry plane,
;;;construct a quadrilateral in the plane *z* = 0 and
;;;add it to the mesh line (see **duplicate 'translation** for details)
(define plane ( make-mesh 'single-point (vector -1 -1 0)))
(duplicate 'translation plane 1 (vector 2 0 0))
(duplicate 'translation plane 1 (vector 0 2 0))
(define my-mesh (make-mesh 'add (list my-mesh plane)))
(view 'mesh my-mesh)

In the medit application use keys 'P' and 'g'.

(duplicate 'rotation. . . )

Description

Constructs a mesh by duplication using a rotation. Points are extruded into lines, lines into quadri- laterals and quadrilaterals into hexahedras.

Syntax

(Duplicate 'rotation mesh rep. rotation-axis orig angle)

Parameters

mesh The mesh to be extruded by rotation. This mesh could be made of by points, lines or quadrilaterals. rep. Number of extrusion. rotation-axis Axis of rotation. For instance the z-axis can be given by the vector (vector 0 0 1). orig Origin of the rotation. The origin (x=0, y=0, z=0) is specified by (vector 0 0 0). angle Angle of rotation in degrees.

Examples

Duplicate a point into lines by rotation

Define a mesh named my-mesh which contain a single point giving its coordinates:

(define my-mesh ( make-mesh 'single-point (vector 0.1 0 0)))
;;;Here the coordinates of the point are (x=0.1, y=0, z=0).
;;; Duplicate the point into lines:
(duplicate 'rotation my-mesh 5 (vector 0 1 0) (vector 0 0 0) 30)
;;;The mesh my-mesh is now an arc which contains 5 lines generated
;;;by rotation of angle 30 degrees around the y-axis.
;;;Visualize the mesh:
(view 'mesh my-mesh)

Duplicate a line into quadrilaterals

Define a line by translation of a point (see duplicate 'translation. . . ). (define my-mesh ( make-mesh 'single-point (vector 0 0.1 0))) (duplicate 'translation my-mesh 1 (vector 0 0.O5 0)) (view 'mesh my-mesh)

Duplicate this line into quadrilaterals (duplicate 'rotation my-mesh 7 (vector 1 0 0) (vector 0 0 0) 10) (view 'mesh my-mesh) The mesh my-mesh is now a surface which contains 7 quadrilaterals generated by rotation of angle 10 degrees around the x-axis.

Duplicate quadrilaterals into hexahedras

Using the quadrilaterals from the previous example generate hexahedras by rotation (define my-mesh ( make-mesh 'single-point (vector 0 0.1 0))) (duplicate 'translation my-mesh 1 (vector 0 0.05 0)) (duplicate 'rotation my-mesh 7 (vector 1 0 0) (vector 0 0 0) 10) (duplicate 'rotation my-mesh 6 (vector 0 0 1) (vector 0 0 0) 15) (view 'mesh my-mesh)

The mesh my-mesh is now a volume which contains 42 hexahedras generated by rotation of angle 15 degrees around the z-axis.

(duplicate 'translation. . . )

Description

Constructs a mesh by duplication using a translation. Points are extruded into lines, lines into quadrilaterals and quadrilaterals into hexahedras.

Syntax

(Duplicate 'rotation mesh rep. translation-vector)

Parameters

mesh The mesh to be extruded by translation. This mesh could be conatin points, lines or quadrilaterals. rep. Number of extrusion. translation-vector vector of translation. For instance translation in the z-direction of length O.1 meter is given by the vector (vector 0 0 0.1).

Examples

Duplicate a point into lines by translation

Define a mesh named my-mesh which contain a single point giving its coordinates:

(define my-mesh (make-mesh 'single-point (vector 0.1 0 0)))
;;; Here the coordinates of the point are (x=0.1, y=0, z=0).
;;;Duplicate the point into lines:
(duplicate 'translation my-mesh 5 (vector 0 0.1 0))
;;;The mesh my-mesh is now a line which contains 5 segments of
;;;length 0.1 meter generated by translation along the y-axis.
;;;Visualize the mesh:
(view 'mesh my-mesh)

Duplicate the previous line into quadrilaterals

(duplicate 'translation my-mesh 2 (vector 0 0 0.2))
(view 'mesh my-mesh)

The 5 segments generate, in the z-direction, a surface mesh named my-mesh of 10 quadrilaterals (5 × 2). Each quadrilateral has a surface of 0.1 × 0.2 meter^2^.

Duplicate the previous quadrilaterals into hexahedras

Take the quadrilaterals from the previous example and generate hexahedras by translation (duplicate 'translation my-mesh 6 (vector -0.05 0 0)) (view 'mesh my-mesh)

The mesh my-mesh is now a volume which contains 60 hexahedras generated by translation of the previous surface in the x-direction.

(define my-mesh ( make-mesh 'read-from-file \"diapason.mesh\"))
(view 'mesh my-mesh)

(make-mesh 'restrict-edge)

Take an edge (or several edges) from a mesh to make a new mesh. This function is helpful to extract a sub mesh from an original mesh. The result is an edge (or a list of edges).

Description Syntax

(make-mesh 'restrict-edge mesh edges)

Parameters

mesh The original mesh from which a sub mesh is extracted. edge(s) The edges to be extrated given by a vector of number of nodes

Example

(define sub-mesh (make-mesh 'restricted-edge (vector 1 2 3 4 1)))

(make-mesh 'restrict-plane)

Description

Take all the quadrilaterals that belong in a plane from a mesh. This function is helpful to extract a sub mesh from an original 3D mesh. The result is a mesh of quadrilaterals.

Syntax

(make-mesh 'restrict-plane mesh normal invariant-point )

Parameters

mesh The original mesh from which a sub mesh is extracted. normal The vector normal to the plane. invariant-point Any point in the plane.

Example

(define sub-mesh (make-mesh 'restrict-plane my-mesh (vector 1 0 0) (vector 0 0 0)))

(make-mesh 'restrict-point)

Description

Take a point (or several points) from a mesh to make a new mesh. This function is helpful to extract a sub mesh from an original mesh.

Syntax

(make-mesh 'restrict-point mesh point(s))

Parameters

mesh The mesh from which the point (or list of point) is (are) extracted. point(s) The point (or a list of point) given by its (their) number(s) in the mesh (see wiew 'mesh to visualize the numbering).

Example

Build your own mesh using the mesh tools: duplicate. . . , add, make-mesh. . . ) or simply read a file (for example diapason.mesh) and visualize it

(define diapason (make-mesh 'read-from-file \"diapason.mesh\"))
(view 'mesh diapason)

Extract a point (define point3 (make-mesh 'restrict-point diapason 3)) or a list of point (define points (make-mesh 'restrict-point diapason (vector 1 2 3))) to define two finite element objects blocked by different ways (define fem1 (make-object 'finite-element (mesh diapason) (block point3))) (define fem2 (make-object 'finite-element (mesh diapason) (block points))) Visualize the objects (view 'object fem1) (view 'object fem2) Use the key 'c' and 'g' in the medit application to see the choosen boundaries.

(make-mesh 'restrict-quadrilateral)

Take an quadrilateral from a mesh to make a new mesh. This function is helpful to extract a sub mesh from an original mesh. The result is a quadrilateral.

Description Syntax

(make-mesh 'restrict-quadrilateral mesh quadrilateral)

Parameters

mesh The original mesh from which a sub mesh is extracted. quadrilateral(s) The quadrilateral to be extrated given by a vector of its nodes

Example

(define sub-mesh (make-mesh 'restricted-quadrilateral (vector 1 2 3 4)))

(make-mesh 'single-point)

Description Syntax

(make-mesh 'single-point position-vector )

Parameters

position-vector This parameter gives the coordinates of a point relative to an orthogonal Cartesian coordinate system Oxyz.

Discussion

Starting from a point, a complex finite element mesh can be obtain using the duplicate, transform and add functions (see example numero).

Example

Define a mesh named my-mesh which contain a single point giving its coordinates:

(define my-mesh ( make-mesh 'single-point (vector 0.1 0 0)))

Here the coordinates of the point are (x=0.1, y=0, z=0).

(make-object 'finite-element)

Description

This function is used to create a finite element object. Its sound properties depend on the geometry (mesh), on the material parameters (density, young's modulus , poisson ration, loss parameters) and on boundary conditions (the fixed part of the mesh). The dynamical behavior of this object is described by the modal theory: the number of requested modes can be specified by the user.

Syntax and default

(make-object 'finite-element** (key value))
(make-object 'finite-element (mesh my-mesh)
                             (block my-sub-mesh)
                             (modes 40)
                             (density 7800)
                             (young 2e11)
                             (poisson 0.3)
                             (freq-loss 1)
                             (const-loss 1))

Parameters

key Value mesh The mesh of the finite element object. This mesh can be obtained using the function make-mesh and the Modalys's mesh tools: duplicate, transform. For the time being, Modalys is able to deal with only one type of finite element: hexahedra. Thus, the user must give here a mesh which contains only hexahedras. In the future, extensions will be made to extend the types of handled finite elements (tetrahedras, beams, plates etc) block The part of the mesh to be constrained. A part (or all) of the surface of the finite element mesh (points, edges or plane) can be fixed during the sound synthesis. The dynamic behavior of an objet (and thus its sound) can be completly different depending on the definition of this fixed topology. This sub mesh can be defined using the function make-mesh 'restrict. . . . key Value modes This value determines the number of modes of vibration computed in the simu- lation of the object. As this number is increased, higher partials are added to the resultant sound. Thus, if ten modes are declared, the lowest ten frequencies pro- duced by the vibration of the object are computed (see funcnamecompute-modes). Maximum detail is obtained when the number of modes is high enough so that all frequency below the Nyquist frequency are accounted for. density Density of the material in kg/m^3^. Some typical values are

+-----------------------+-------------+-----------------+-------------+  
|   Oak                 | 720         | Brass           | > 8500      |  
+:======================+=============+=================+:============+  
|   Glass               | 2300        | > Nickel        | > 8800      |  
+-----------------------+-------------+-----------------+-------------+  
|   Quartz              | 2650        | Copper          | > 8900      |  
+-----------------------+-------------+-----------------+-------------+  
|   Aluminium           | 2700        | > Silver        | > 10500     |  
+-----------------------+-------------+-----------------+-------------+  
|   Steel               | 7700        |                 |             |  
+-----------------------+-------------+-----------------+-------------+

young Young'smodulus, in N/m^2^. This parameter is related to the elasticity of the mate- rial. A rigid material gets higher values. Some typical values are Glass 6.2e10 Brass 1.04e11 Quartz 7.9e10 Nickel 2.1e11 Aluminium 7e10 Copper 1.2e11 Steel 2e11 Silver 7.8e10 poisson Poisson ratio of the material, from 0 to 1. With a value of 1 the material keep a constant volume when a deformation occurs (imagine a ballon plenty of water). Lowered values authorize a loss in the total volume when a compression is done on the material. freq-loss const-loss

Example

Define a mesh named my-mesh to declare a finite element object (see make-mesh, duplicate)

(define my-mesh (make-mesh 'single-point (vector 0.1 0 0)))
(duplicate 'translation my-mesh 1 (vector .013 0 0))
(duplicate 'rotation my-mesh 10 (vector 0 1 0) (vector 0 0 0) 6 )
(duplicate 'rotation my-mesh 59 (vector 0 0.0 1) (vector 0 0 0) 6 )
(view 'mesh my-mesh)
;;;Select a part of the mesh my-mesh
(define my-sub-mesh (make-mesh 'restrict-plane my-mesh (vector 0 0 1)
(vector 0 0 0)))
(view 'mesh my-sub-mesh)

The mesh named my-sub-mesh represents the plane of equation z = 0 (the ground here) re- stricted to the mesh my-mesh

Define a finite element objet using the mesh my-mesh, block the sub mesh my-sub-mesh and ask for 30 modes (define my-fem (make-object 'finite-element (mesh my-mesh) (block my-sub-mesh) (modes 30))) (view 'object my-fem) To visualize the mesh and the sub mesh use 'c' and 'e' in the medit application (see Fig 1). Note that here the material parameters (density, young, poisson) and the losses are given by default. Figure 1: To obtain the number of a node, visualize the finite element object using the view 'object command and shift click the facet of interest

Notes

The function make-access (see Modalys Reference) can be used on a finite element object. Three direction can be declared: 'normal, 'trans0 or 'trans1. For example the instruction (define my-fem-access1( make-access my-finite-element (const 1298) 'normal )) make an access on the 1298th node of the finite element mesh in a direction normal to its surface. An access can be declared in the tangential direction of the surface giving two node numbers: (define my-fem-access1( make-access my-finite-element (const 1298 1285) 'trans0 )) An access is created at node 1298 in the tangent plane pointing through the node 1285. Using 'trans1 the access is still in the tangent plane but point in the perpendicular direction. To obtain a node number, see the figure 1). The medit application can return, in the console, the coordinates of the vertex involved in a facet and their numbers within the mesh: Picking result : Quad 731 : 1298, 1287, 1273, 1285 ref : 0 [DEFAULT_MAT]

+----------+----------+------------+-----------+------------+-----+-----+
| > vertex | 1298 :   | > 0.105121 | 0.034156  | 0.023494   | ref | > 0 |
+:=========+=========:+============+===========+============+====:+=====+
| > vertex | 1287 :   | > 0.102209 | 0.033210  | 0.034919   | ref | > 0 |
+----------+----------+------------+-----------+------------+-----+-----+
| > vertex | 1273 :   | > 0.098178 | 0.043712  | 0.034919   | ref | > 0 |
+----------+----------+------------+-----------+------------+-----+-----+
| > vertex | 1285 :   | > 0.100975 | 0.044957  | 0.023494   | ref | > 0 |
+----------+----------+------------+-----------+------------+-----+-----+

All the functions make-connection . . . can be used with a finite element object (except make- connection 'hole that does not make sens). A finite element object can be stroke, bowed, plucked, . . . with an other Modalys object included an other finite element object.

(save-mesh)

Description

Save the mesh data in a file

Syntax

(save-mesh mesh filename)

Parameters

mesh Name of the mesh to be saved filename name of destination file (in quote)

Example

Create a mesh named my-mesh using the mesh tools (see duplicate 'rotation for example) and save the mesh

(save-mesh my-mesh \"rotate.mesh\")

Keep in mind that the file format is the INRIA mesh format.

(set-physical)

Description

Set some material properties to a finite element object . This function can be used to avoid to redefine a finite element object. The function compute-mode must be apply in order to take into consideration the new material properties.

Syntax and default

(set-physical modalys-object (key value)) (set-physical my-object (density 7800) (young 2e11) (poisson 0.3))

Parameters

modalys-object The modalys object to be updated. key Value density Density of the material in kg/m^3^. Some typical values are

+-----------------------+-------------+-----------------+-------------+
| > Oak                 | 720         | Brass           | > 8500      |
+:======================+=============+=================+:============+
| > Glass               | 2300        | > Nickel        | > 8800      |
+-----------------------+-------------+-----------------+-------------+
| > Quartz              | 2650        | Copper          | > 8900      |
+-----------------------+-------------+-----------------+-------------+
| > Aluminium           | 2700        | > Silver        | > 10500     |
+-----------------------+-------------+-----------------+-------------+
| > Steel               | 7700        |                 |             |
+-----------------------+-------------+-----------------+-------------+

See the command

(view 'mode diapason-fem 18 20 5)

in the compute-mode example. Right click in the medit application to obtain the main-menu. Choose 'Play sequence' in the 'animation' sub-menu.

(view 'object)

Description

Visualize an object with the choosen boundaries.

Syntax

(view 'object my-finite-element)

Parameters

my-finite-element The finite element object to be visualized.

Examples

;;; fem-example 
(new) 
(define side 0.002) (define r 7 ) (define s 21 )  
(define h (*2.2 r side ))  
(define base ( make-mesh 'single-point (vector side side 0) ))
(duplicate 'translation base 1 (vector (* -2 side) 0 0))  
(duplicate 'translation base 1 (vector 0 (*-2 side) 0))  
(duplicate 'homothety base 1 (vector 0 0 ( *2 side)) 1 )
(define base_inv (make-mesh 'copy base ))
(transform 'reflection base_inv (vector 0 0 1) (vector 0 0 ( *-2 side )))
(define base (make-mesh 'add (list base base_inv)))  
(define diapason (make-mesh 'single-point (vector side side 0)))
(duplicate 'translation diapason 1 (vector (*-2 side) 0 0))  
(duplicate 'translation diapason 1 (vector 0 (*-2 side) 0))
(duplicate 'translation diapason r (vector 0 0 (*2 side) ))  
(define arc (make-mesh 'restrict-quadrilateral diapason  
(vector (+ 4 (*4 r )) (+ 2 (*2 r)) (+ 1 (*2 r)) ( + 3 (*4 r)))))  
(duplicate 'rotation arc 6 (vector 1 0 0) (vector 0 side h) 15)  
(define branch (make-mesh 'restrict-plane arc (vector 0 0 1) (vector 0 0 h)))
(duplicate 'translation branch s (vector 0 0 (*2 side)))  
(define fork (make-mesh 'add (list arc branch))) (define fork-copy
(make-mesh 'copy fork))  
(transform 'reflection fork-copy (vector 0 1 0) (vector 0 0 0))  
(define diapason (make-mesh 'add (list base diapason fork fork-copy)))
(save-mesh diapason \"diapason.mesh\")  
(view 'mesh diapason )  
(define hold (make-mesh 'restrict-quadrilateral diapason (vector 63 189 188 62)))  
(define my-finite-element (make-object 'finite-element (mesh diapason)  
(modes 25)  
(block hold) (young 19.5e10) (density 7700)  
(poisson 0.2)  
(freq-loss 0)  
(const-loss 0)))  
;(view 'object my-finite-element ) (compute-modes my-finite-element )
(set-mode-freq! my-finite-element 0 0)  
(set-mode-freq! my-finite-element 1 0)  
(save-object my-finite-element \"diapason.modal\" ) (view 'mode my-finite-element 3 10 3 )  
(define my-fem-access-in ( make-access my-finite-element (const 120) 'normal ))  
(define my-fem-access-out ( make-access my-finite-element (const 15) 'normal ))  
(define my-plectrum (make-object 'bi-two-mass))  
;;;  
;;; make pluck connection  
;;;  
(define my-plectrum-plk (make-access my-plectrum (const 1) 'trans0))
(make-connection 'pluck my-fem-access-in my-plectrum-plk 0 .1 (const 50))  
;;;  
;;; make position connection to push plectrum  
;;;  
(define my-plectrum-mov (make-access my-plectrum (const 0) 'trans0))
(make-connection 'position my-plectrum-mov  
(make-controller 'envelope 1  
                  (list (list 0.00 .1)  
                  (list 0.50 -.5))))  
;;;  
;;; make listening point on string  
;;;  
(make-point-output my-fem-access-out)  
;;;  
;;; run the synthesis and play the sound  
;;;  
(run 2) ;; make 2 seconds of sound (play)  
(save \"diapason.aiff\")

★ ★
★

3D Finite Elements

Introduction

(compute-modes)

Description

Syntax

Parameters

Example

See also

view 'mode, make-object 'finite-element

(duplicate 'homothety)

Description

Syntax

Parameters

Example

Duplicate a quadrilateral into hexahedras by homothety

See also

transform 'homothety, make-mesh, view.

(duplicate 'reflection)

Description

Syntax

Parameters

Example

Duplicate a point into a line by reflection with the plane z = 0

See also

transform 'reflection, make-mesh, view.

(duplicate 'rotation. . . )

Description

Syntax

Parameters

Examples

Duplicate a point into lines by rotation

Duplicate a line into quadrilaterals

Duplicate quadrilaterals into hexahedras

See also

duplicate 'translation, make-mesh, transform, view.

(duplicate 'translation. . . )

Description

Syntax

Parameters

Examples

Duplicate a point into lines by translation

Duplicate the previous line into quadrilaterals

Duplicate the previous quadrilaterals into hexahedras

See also

duplicate 'rotation, make-mesh, transform, view.

(make-mesh 'add)

Description

Syntax

Parameters

Example

See also

duplicate 'reflection

(make-mesh 'copy)

Description

Syntax

Parameters

Example

See also

(make-mesh 'read-from-file. . . )

Description Syntax

Parameters

Discussion

Example

See also

view, make-mesh, medit.

(make-mesh 'restrict-edge)

Description Syntax

Parameters

Example

See also

(make-mesh 'restrict-plane)

Description

Syntax

Parameters

Example

See also

(make-mesh 'restrict-point)

Description

Syntax

Parameters