Skip to content

Bilinear (1st Order IIR) Filter

Description

Filters its inputs by a first order IIR (Infinite Impulse Response) filter controlled by a set of 3 coefficients.

Syntax and Default Values

The bilinear-filter controller can be created using the following Mlys (Max), mlys.lua, or Lisp syntax:

In Modalys for Max, this object is named mlys.bilinear-filter:

An input controller must be connected to the first inlet.
The dimension is automatically the same as the input controller.
💡 If a second inlet is given, you can connect a 3-dimensional controller encapsulating the 3 coefficients of the filter. Otherwise a dynamic controller will be created automatically.

modalys.create_controller{kind="bilinear-filter",
                          coefficients={2.3,0,1.5},
                          input=<controller of any dimension>,
                          name="MyBilinearFilter"}

The dimension is automatically the same as the input controller.
The coefficients parameter can be a controller (3-dimensional), but if passed as a table of 3 values, it can be modified dynamically via Max messages with MyBilinearFilter@coefficients

(make-controller 'bilinear-filter
                  dimension
                  coefficients
                  input)

Parameters

This controller takes 3 parameters:

  • dimension: number of dimensions of the input and output controllers (automatic for mlys.lua and Modalys for Max).
  • coefficients: a 3-dimensional controller specifying the 3 bilinear filter coefficients.
  • input: filter input (a controller).

dimension must be the same as the input controller's dimension.
The coefficients controller should be 3-dimensional representing the a0, a1 and b1 coefficients.
This controller is updated at every sample (period = 0).

Discussion

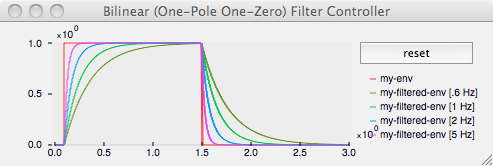
This filter implements a general first-order (one-pole one-zero) filter which can be used for a variety of purposes, including smoothing out envelopes, and filtering sound-file, signal or other controllers. The following example (in Lisp) is shown in one of the graphs (with a 1 Hz cutoff) in the above image:

(setq sp (get-info 'sample-period))
(setq my-env (make-controller 'envelope 1 
         (list '(0 0.0) '(0.1 0) (list (+ 0.1 sp) 1) '(1.5 1) (list (+ 1.5 sp) 0)) ))
(setq cutoff 1)
(setq val (sin (* cutoff 2 pi sp)))
(setq my-coef-ctl (const (list val 0 (- val 1))))
(setq my-filtered-env (make-controller 'bilinear-filter 1 my-coef-ctl my-env))
You should probably consider using it or the biquadratic-filter, instead of the older filtering functions. However, you will need to generate your own sets of coefficients from higher level parameters such as center/cutoff frequency, etc....


★     ★
★