Introduction
Definitions
A spectral envelope is a curve in the frequency-amplitude plane, derived from a Fourier magnitude spectrum. It is a function of frequency that matches the amplitudes of the individual partials of the spectrum. It is the basic defining factor for its timbre. The envelope changes over time and can change with the fundamental frequency of the sound.
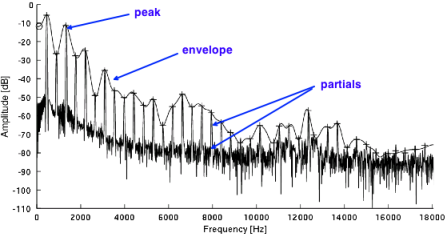
More specifically, the spectral envelope is based on a smooth function that passes through the prominent peaks of the spectrum.
There are several methods of spectral envelope analysis. These were developed in link with the analysis of speech. The part of the spectral envelope is crucial in the recognition of vocal sounds, due to the formants that characterize the timbral quality of vowels. A spectral envelope has a number of characteristics.
Envelope fit : the curve wraps tightly around the magnitude spectrum linking its peaks.
Regularity : the spectral envelope must give a general idea of the distribution of the signal's energy over frequency
Steadyness : in the mathematical sense of the term : it has no corners.
In AudioSculpt, the spectral enveloppe of a sound can be visualized with several algorithms.
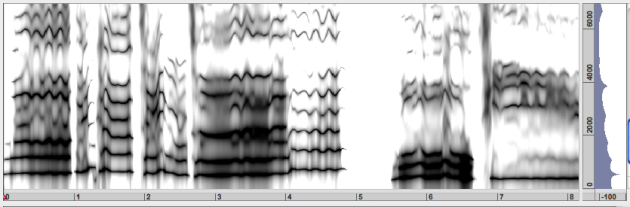
LPC : Linear Predictive Coding
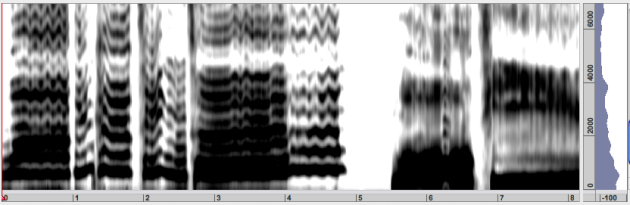
True Envelope : an improvement of LPC, which is especially relevant to discriminate low and high frequencies.
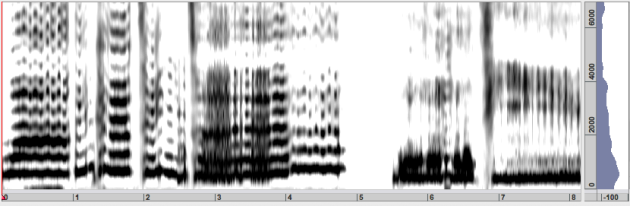
Discrete Cepstrum, a variante of the Cepstrum analysis.
Spectral Envelope Estimation
There are two ways to explain the spectral envelope estimation.
A Fourier magnitude spectrum is calculated, and the curve is smoothed successively to get an envelope, without unsignificant fluctuations, as if a low pass filter was applied to the spectrum. The slow fluctuations only – low frequency oscillations – pass.
According to the source-filter model of speech production, a speech signal can be expressed as a convolution between an excitation signal produced by the glottis, and the impulse response of the vocal tract filter. The source spectrum is separated from the filter transfer function, yielding an estimation of the spectral envelope.
