Discrete Cepstrum
The cepstrum ( /ˈkɛpstrəm/ ) name was derived by reversing the first four letters of "spectrum". The discrete cepstrum method is derived from the cepstrum envelope estimation. expresses the rate of change in the different spectrum bands: the Fourier transform of the spectrum is considered as a signal. It is more suitable for the representation of nearly periodic sounds than LPC or the cepstrum.
Discrete Cepstrum Method
Like the LPC or true envelope, the discrete cepstrum spectral envelope analysis is a method of speech analysis based on the source-filter model of speech production. The pitch and the formants are separated very clearly.
The discrete cepstrum yields a spectral representation of the signal from the spectral peaks of a sound, which will most often be the sinusoidal partials found by additive analysis.
The cepstrum analysis has a specific parameter : cepstrum coefficients, or CED. These coefficients are especially relevant from a perceptual point of view. They model the spectral energy distribution. They are computed from sinusoidal peaks in the short time spectrum.
The cepstrum envelope estimation is based on a Fourier magnitude spectrum. The curve is smoothed successively to get rid of its fluctuations. This amounts to applying a low pass filter to the spectrum, interpreted as a signal. The slow fluctuations only – low frequency oscillations – pass. The source spectrum is separated from the filter transfer function, yielding a very good estimation of the spectral envelope.
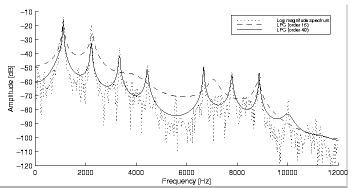
As a low pass filter, the cepstrum method averages-out the fluctuations of the curve of the spectrum. The cepstrum follows the curve of the spectrum down to the residual noise level in the gap between two partials in analysing harmonic sounds, or partials spaced too far apart. The resulting envelope will reach the level of residual noise between partials which are spaced too far apart. The resulting curve has no longer the enveloping property to link the peaks of the curve.
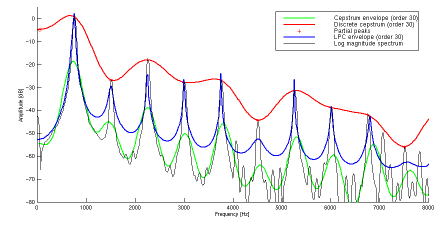
Contrary to LPC and cepstrum methods, the discrete cepstrum spectral envelope is computed from spectral peaks which do not have to be regularly spaced in frequency. It only cares about the partials of the signal. It generates a smoothly interpolated curve which tries to link the partial peaks. The resulting envelope is smoother.
The CED Order parameter defines the number of coefficients to compute. If the number of coefficient is too low, the enveloppe will be irrelevant. If the number is too high, the envelope follows the spectra too closely.
By default, the number of coefficients is equal to 30. It can be calculated as follows :
N< SR/(f0max*0.5)
The discrete cepstrum analysis is slower than the true envelope analysis. It is less effective for treatments requiering the preservation of the spectral envelope.
Exemple : CED and Resolution
Cepstral Advanced Concepts
The quefrency is a measure of time. For example, with a 44100 Hz sampling rate with a large peak of 100 samples in the cepstrum, the peak indicates the presence of a pitch that is 44100/100 = 441 Hz. This peak occurs in the cepstrum because the harmonics in the spectrum are periodic, and the period corresponds to the pitch. Note that a pure sine wave should not be used to test the cepstrum for its pitch determination from quefrency as a pure sine wave does not contain any harmonics.
A filter that operates on a cepstrum might be called a lifter. A low pass lifter is similar to a low pass filter in the frequency domain. It can be implemented by multiplying by a window in the cepstral domain and when converted back to the time domain, resulting in a smoother signal.
The convolution of two signals can be expressed as the addition of their cepstra.