IntroductionHiérarchie de section : Signal Analysis > Signal Analysis Introduction > Preliminary Notions > Fourier TransformFourier Transform
Jean Baptiste Joseph Fourier (1768 – 1830) was a french mathematician and physicist who defined the Fourier series, which can apply to vibrations. As far as we are concerned, he demonstrated that any time varying function can be divided in single periodic signals.
The Fourier Series
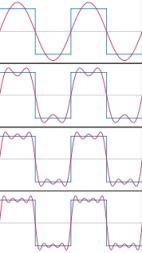 The first four Fourier series approximations for a square wave. | A Fourier series decomposes any periodic function or periodic signal into the sum of simple oscillating functions. Any function which changes in time can be divided in single periodic signals. A non periodic signal can be considered as a succession of periodic portions of this signal. The Fourier transform can then also apply to non periodic signals, step by step, to allow this decomposition on each portion of the signal. |
The Fourier Transform is an algorithm that can be used for the decomposition a sequence of values – an digital audio signal, for instance – into components of different frequencies. Hence, it can be applied to analyse the spectral components of a sound. The Fast Fourier Transform is a variante of the Fourier Transform, which allows the fast calculus of the components.
Analysis Window
Because the analysis is done step by step, it is based on a window. This window is applied to a number of signal samples, which determines its width, or size.
Windows are applied successively in time to the signal until the whole file is analysed. The number of samples of each window is also divided in bars, or "bins". The number of bins is proportional to the number of samples in the window : it is the FFT size, which reminds us of the main principle of the Fourier Series. Consequently, the window size and the FFT size determine the resolution of the representation in frequency and time.
To perform an efficient analysis, windows overlap. This "space" between each window is called the window step. To avoid clicks when overlapping the windows, the windows have a windowing curve, which defines the window type. These parameters interact with the sample rate of the signal.
