OpenMusic DocumentationHiérarchie de section : OM 6.6 User Manual > Visual Programming II > Abstraction > Recursive Patches > Recursive TreesRecursive Treatment of Tree Structures
Recursive Treatment of Tree Structures
Recursion is often applied to tree structures, such as lists. Indeed, a list can be described as a tree, whose components are either leaves , or nodes . A leaf is a termination of a tree, a node is another list that can, also, contain leaves of nodes.
We would like to add 1 to each number in a tree with many sublists : 1 + ( ((1 2 3)(4 5 6)) (4) ((6 7))) ) .
In other words, we want to increment – increase the value of – the terminal items of the list. But we cannot just apply om+1 to the list : om+ cannot reach each atom directly. It must go through each level of the tree.
We will apply the following recursive function to the tree : IncrListElements (LIST) = for each ELEMENT in the LIST, do :
- "If element is an atom, then return element + 1." This is the termination condition.
- "Else, apply IncrListElement to the elements." This is the recursive call to IncrListElements.
The whole tree is ran through and all terminal items are incremented. Hence, the termination condition of a recursive function, when applied to a tree structure, is to reach a leaf, or extremity of a tree.
This patch illustrates the previous case :
"Input" yields values or lists of values to be processed.
If an element is an atom, "input" is incremented directly.
If an element is not an atom, – that is, a list –, the patch is applied recursively to each element of the list...
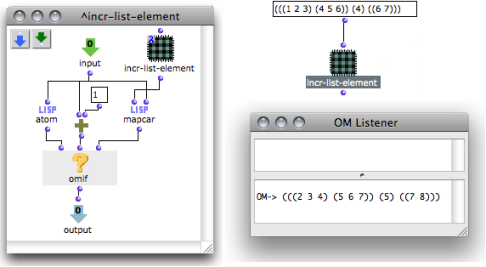
Mapcar allows to apply the patch on "lambda" mode successively to each element of a list. An alternative would be using an OMLoop to call the sub patch successively on each element of the list.
