Recherche Google
OpenMusic DocumentationOM 6.6 User Manual > Visual Programming II > Higher-Order Functions > Test Functions
page précédentepage suivante

Lambda Mode Examples: Test Functions

Some functions have a test argument. This test argument determines the way the function operates on data. For instance, it can set comparaison rules for a sorting process, conditions to fulfill reject items from a list, etc.

This test can therefore be modified by specifying a function, or more generally a lambda function, which allows to modify the behaviour of the initial function.

Example : Removing Duplicates in a List

The remove-dup function tests if the items of a list are equal pairwise, and if so, removes duplicates from the pair.

  • Its first argument is a list.

  • Its second argument is a test function. This test function determines the nature of the "equal" test. It has a default value : 'eql. Values are compared with the Lisp eql function.

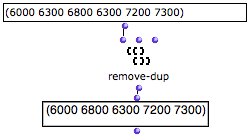
removing duplicates : One of the two occurences of 6300 has been removed from the input list.
removing duplicates : One of the two occurences of 6300 has been removed from the input list.
Defining a New Test Function

We would like to remove octaves from a list of pitches, but there is no such function in OM. To do so, we can use remove-dup with a new test function that can detect octaves in the input pitch list. For instance, the previous example has two duplicates : 6000 and 7200, a C4 and a C5.

Values can be considered equal according to the octave interval, if they are compared modulo[1] the octave interval .

Note that an octave = 1200 cents.

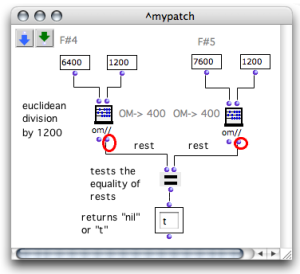
The following patch tests if the pitches are equal modulo an octave with the function om//.

  • The first output of om// returns the quotient of the division.

  • The second output returns the remainder of the division.

The = predicate tests if the remainders of the division by 1200 of two elements are equal, that is, if these two elements are equal modulo 1200.

Modulo and Octave

  • Two values are "equal the same modulo" when their division by the same divisor produces the same remainder .

    An octave = 1200 cents. If two values are "equal modulo 1200" they have an octave relation. This mieans that an euclidean division by 1200 should return the same remainder. 

  • For instance : C4 is equal to 6000, C5 to 7200. F#4 is equal to 6400, F#5 to 7600.

    C4 : (6000 / 1200) = 5, remainder 0

    C5 : (7200 / 1200) = 6, remainder 0

    F#4 : (6400 / 1200) = 5, remainder 4

    F#5 : (7600 / 1200) = 6, remainder 4

Modifying the Function Behaviour

The new test function can now become the test argument and replace the defautt eql test of remove-dup .

  • The patch, now on "lambda" mode is connected to remove-dup as a test argument.

  • The two inlets of the patch indicate that the lambda function takes two arguments.

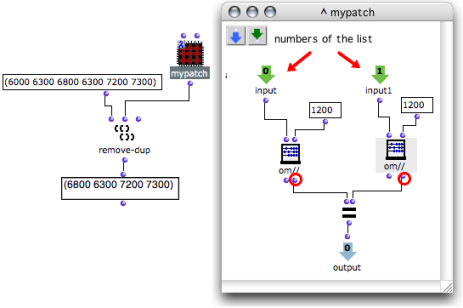
Remove-dup can now remove all values whose modulo 1200 is equal to the modulo 1200 of another value.
Remove-dup can now remove all values whose modulo 1200 is equal to the modulo 1200 of another value.
Lambda Patch
General Issues with Lambda Functions
  1. Modulo

    In computing, the modulo operation finds the remainder of division of one number by another. If two numbers, a and b , when divided by the same n divisor, have the same remainder, they are "equal modulo n ".

    -> If remainder ( a  / n ) = remainder ( b / n ), a = b , modulo n .

page précédentepage suivante
A propos...(c) Ircam - Centre PompidouRéalisé avec Scenari