Recherche Google
OpenMusic 6 – User ManualAdvanced Visual Programming > Evaluation Modes > Lambda Mode > Lambda / Higher-Order Functions
previous pagenext page

Applying a Lambda Function via a Higher-Order Function

A higher-order function basically takes two arguments : a function, that is, a functional argument, and another argument. The functional argument is applied to the second argument by the higher-order function.

Basic Principles

  1. The functional argument is a variable of the higher-order function.

  2. The functional argument must be added one "free" input per supplemental arguments of the higher-order function.

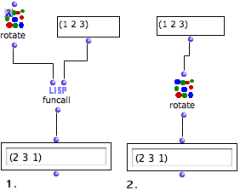
We will show the application basis of a lambda function via a higher-order function to another argument.

Applying Rotate to a List via Funcall

We will use funcall as a higher-order function, the rotate function as a first argument, and a list as a second argument. This means that rotate is now a variable of funcall.

  • Funcall, – "fun" stands for "function" – makes function calls : it applies a function to a second argument.

  • Rotate returns the circular permutation of a list : it enumerates the items of a list starting from the second element.

  1. A free input is added to rotate so that it is applied to the list. Funcall is the higher-order function. Rotate is on "lambda" mode. Funcall applies rotate to the list.

  2. Rotate is not on "lambda" mode anymore. It takes the same list as argument.

Note

The result of the computation is the same in both cases. We will now extend the previous example to show how using a function as an actual variable.

Random Application of Two Functions to a List

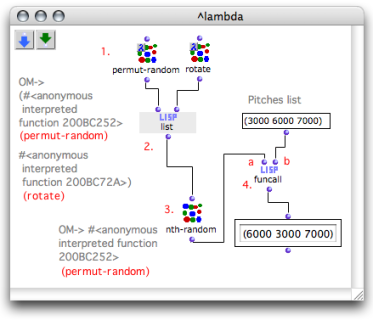
Using lambda functions allows to choose randomly between two functions to apply to another argument. Here, we want to modify a list of values with one of two functions that would be selected randomly. in other words, we would like this function to be a random variable . We will apply either permut-random, or rotate to a list.

  • Permut-random makes a random permutation of the elements of a list.

  • Rotate enumerates the elements of a list from the second element.

"Permut-random" is applied randomly to the list.
"Permut-random" is applied randomly to the list.

  1. Permut-random and rotate are our variables : they are set on "lambda" mode.

  2. List makes a list with these two functions .

  3. Nth-random picks one of the two functions in the list randomly.

  4. Funcall is the higher-order function that applies this function as a first argument to its second argument, a list.

Note

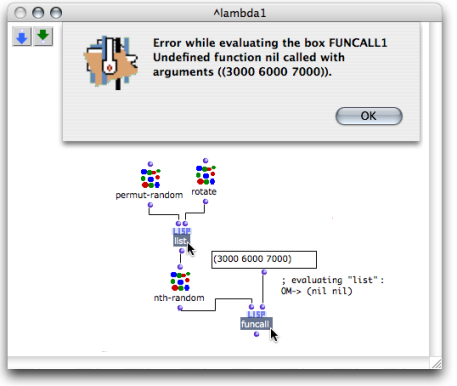
Making a list with two functions, and choosing one of them in the list like a "lambda item" is possible precisely because these functions are on "lambda" mode.

If the two functions were not on "lambda" mode, the list function would return a list that contains the result of these functions call.
If the two functions were not on "lambda" mode, the list function would return a list that contains the result of these functions call.

Inputs of a Lambda Function

A lambda function can be applied to several arguments. Hence, calculations can be executed upon arguments the lambda function may not take otherwise.

"Free" Inputs of a Lambda Function

A function on "lambda" mode must have as many "free" inputs as arguments returned by the higher-level function.

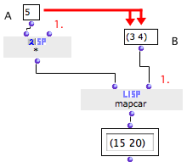
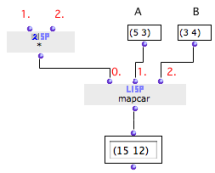The * function cannot multiply lists, like om*. To multiply the elements of two lists, we will apply * with mapcar.

Mapcar applies a function to the first element of each next input, then to the second argument, to the third argument, and so on, and builds a list with the result of each evaluation.

  • Input #0 of mapcar is the * function.

  • Inputs #1 and 2 of mapcar match inputs #1 and #2 of * on "lambda" mode.

  • The resulting lambda function can be expressed as follows : ( x ) * ( y ), where x and y are the successive elements of each list.

Note that the two inputs of om* remain free.

Adding a Default Argument to a Lambda Function : "Currying"

Currying

"Currying" is the reduction of the number of arguments of a lambda function by assigning it one default argument.

Default Argument

This default argument must belong to the arguments accepted by the function : the function has predefined and undefined arguments. The number of inlets of the higher-level function must take the number of free inlets into account.

Here, * has

  • one default argument : a number

  • one free input, which represents the second input of mapcar.

Remember that * only accepts numbers.

  1. Mapcar goes through the second input list (B).

  2. It "tells" the * function to apply (A) to the each item of (B) successively.

  3. The lambda function that is built can be expressed as follows :

    ( 5 ) om* ( x ), where x stands for the elements enumerated through (B).

previous pagenext page
About...(c) Ircam - Centre PompidouMade with Scenari