@linearize(nim, tol:numeric)
tol (i.e. for any point in the
domain, the images of the nim argument and the image of the resulting nim are withing tol) .
The result is a linear homogeneous nim.
The application of the @linearize function can be time consuming and
care must be taken to not perturb the real-time computations, e.g., by
precomputing the linearization: see [eval_when_load] clause and function
@loadvalue.
See also @align_breakpoints, @sample and the nim simplification functions: @simplify_radial_distance_t, @simplify_radial_distance_v, @simplify_lang_v, @filter_median_t, @filter_min_t, @filter_max_t, @window_filter_t
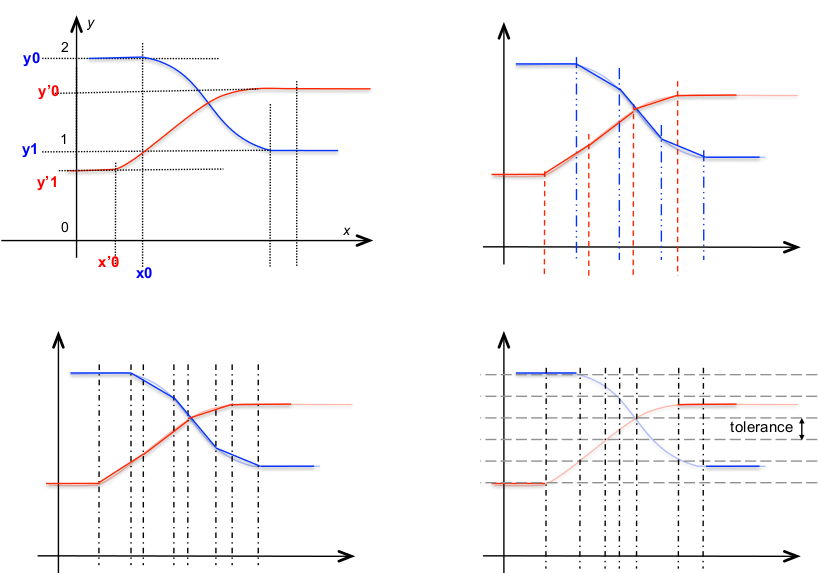
In the figure below, the diagram at the top left shows a vectorial nim with two components:
-
the effect of
@sampleis pictured at top right, -
the effect of
@align_breakpointsis sketched at bottom left, -
and the effect of
@linearizeis illustrated at bottom right.