An Introduction to Modalys
Nearly a quarter of a century has passed since the very first version of Modalys (originally named Mosaic) was developed at IRCAM. The program was initially created by Jean-Marie Adrien for his doctoral thesis in Physics and subsequently redesigned by Joseph Morrison coded in C++, but using an interactive text-based user interface in the Scheme programming language (a cousin of Lisp) as a control mechanism. As processor speeds increased in the decades that followed, Modalys was extended and improved by a host of other developers: Gerhard Eckel, Francisco Iovino, Nicolas Misdariis, Christophe Vergez, Nicholas Ellis, Joël Bensoam and Robert Piéchaud. Since then, the original user manuals and reference, written by Joseph Morrison and David Waxman (with some later updates and editing by Gerhard Eckel, Francisco Iovino and Marc Battier) had become horribly out of date and due to changes, improvements and additions to the program, and consequently the documentation was both missing important descriptions of new features and contained descriptions of existing features which no longer reflected their actual syntax.
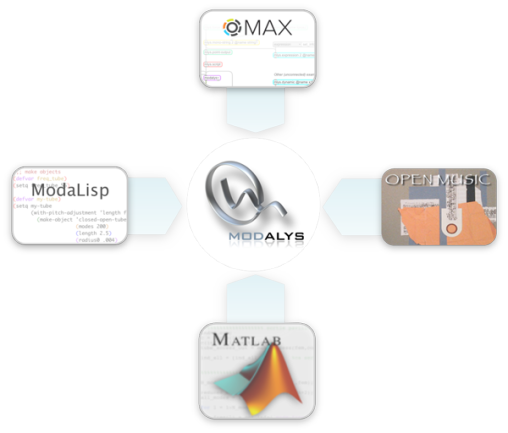
For the moment this new manual refers mainly to the syntax of the current Lisp interface, ModaLisp. Since other interfaces to the Modalys calculation engine (i.e. the Open Music (OM) Modalys interface, as well as the modalys~ and MLYS interfaces for Max/MSP) follow this syntax, it seemed to make sense to focus initially on the Lisp interface, since it serves as a common denominator for all flavors of Modalys.
In addition to the above-mentioned people, special thanks also go to René Caussé, Mikhail Malt, Jean Lochard, Manuel Poletti, Hans Peter Stubbe Teglbjærg and Karim Haddad, who helped to provide examples as well as to unearth long-lost Modalys-related documentation and other materials from their archives.
Richard Dudas, 2012/13
Hanyang University, Seoul
Modalys is a physical modeling synthesis program. In computer music, physical modeling synthesis methods has been a good way of obtaining qualities of sound which are not easy to produce with standard sound synthesis methods such as additive, subtractive or frequency modulation.
A sound wave is the result of a mechanical or acoustical vibration of a body. The vibration results from an external source which injects energy into the body, for instance a hammer striking a membrane or the flow of air perturbing a pipe. Usually the object source of energy is referred to as the “exciter” and the vibrating object is called the “resonator.” The type of coupling between the two objects is known as an “interaction.”
Most types of sound can be decomposed into two opposing categories: transient sounds whose perceptual characteristics evolve quickly in time, and stationary sounds whose perceptual characteristics evolve slowly in time. Sounds in the latter category are easy to reproduce with the computer since the Fourier theory gives us powerful methods to decompose and generate static periodic signals. Traditional synthesis methods are related to the Fourier theory and are thus appropriate for generating stationary sounds. Unfortunately, the Fourier theory has some limitations when dealing with transient sounds, so alternative methods (filtered noise and other non-periodic synthesis methods) have been proposed as computational tools for generating sounds in this domain.
Physical modeling programs generate sounds which are the result of a numerical simulation of vibrating structures represented numerically inside the machine. In particular the program can simulate simple structures such as strings, pipes and plates, but also complex ones such as a cello body or a clarinet mouthpiece. Classical physical modeling techniques rely on space discretization - in other words, in order to simulate a certain structure the computer represents it as a set of masses distributed uniformly in the space. The principal problem of this approach is that the representation is always dependent on the spatial properties of the structure and thus each structure needs an individual type of representation.
The means by which the Modalys program generates the sound is called modal synthesis. Modal synthesis is a musical application of modal theory which arises from the aircraft and bridge-building industry, where precise simulation of vibrating structures submitted to external forces is needed. The basic result of Modal theory is that the way a structure will react to a given external excitation can be predicted by knowing which are the basic modes of vibration of the structure. A mode of vibration is defined as a particular shape the structure assumes when it is excited by a periodic force at a certain frequency and all its points resonate at that frequency. One of the fundamental principles of acoustics states that any vibration of a structure can be decomposed as a superposition of its basic modes of vibration. Modal theory has also developed experimental methods for measuring the modes of vibration of a given musical instrument. Compared with the existing physical modeling synthesis methods, modal synthesis offers two advantages:
• representation is independent of the spatial properties of the structure. This is especially useful since continuous transition from one instrument into another reduces the transition of modal parameters.
• representation is directly related to the aural characteristics of the structure. The resonating frequencies of a mode are the spectral components of the sound produced when exciting the structure with an impulse.
To understand the idea of Modalys synthesis, imagine yourself as an instrument maker (luthier), sitting at a large empty workbench. In the drawers of the bench, there is an unlimited supply of objects which you can put upon the table and assemble into instruments. Objects, in most cases, can be thought of as real physical entities which can be glued together, struck, plucked, bowed, or otherwise excited in order to produce vibrations, and in turn, sounds. They include strings, air columns, two-mass models (which act as hammers, picks or fingers depending on their sizes), metal plates, membranes, violin bridges, and cello bridges.
Suppose that we would like to make a simple instrument which has one string. Our first difficulty arises when we open the workbench drawer labeled “Strings.” Unlike the real-world instrument maker, who might have a small drawer containing 20 different kinds of strings varying in size, material, length, and thickness, we have a very large drawer. It is, in fact, an infinitely large drawer from which we can take a string of any material and dimension. When choosing our string, then, we must be very specific about its parameters. Later in this manual, we will go into more detail on this subject; for the moment, imagine that we know exactly which string to take from the drawer and we put it on the table. String objects in Modalys come with their ends fastened securely against virtual “walls,” so we don't have to worry about making a body for the instrument. We can add one later if we want.
To play the string, we must first make several choices: what object do we use to excite the string (a finger, a pick, a reed, or a sledgehammer, to name a few possibilities), and how do we excite it. The possible answers to our first question are numerous; in fact, a Modalys object can be excited using any other Modalys object. Most of the the types of objects which one normally uses to excite a string are variations of the two mass model (i.e., fingers, picks, hammers, bows, etc.), but one can also use other objects such as air columns, and metal plates. Let us, for now, open the drawer labeled “Two-Mass Models” and pull out a guitar pick. We now face the second question of what to do with the pick. Modalys permits several interactions, called connections, between objects. Connections can be thought of as black boxes which go between objects specifying a certain relationship between them. For example, two objects may be “glued” together, one object may bow another, pluck another, strike another, or push another. All of these interactions: glue, bow, pluck, strike, and push are connection types (the complete list of possible connection types will be presented below). Each connection can be piloted using controllers, which can be conceptualized as knobs which specify exactly how the connection will be executed. A bow connection must be told, for example, how much rosin is on the bow, how fast to move the bow across the string, etc. Controllers can either be told to maintain a constant value, or can be changed dynamically during the synthesis.
Returning to our workbench surface, we see a string, a pick, and a black box with a few knobs on it and the label “pluck.” To finally connect them together we must specify where the objects will physically interact. For instance, do we want to pluck the middle of the string or near the end? Do we want to pluck with the small end of the pick or the large end? To specify a physical location on a Modalys object so that it can interact with other objects, we make what is called an access. The above instrument will require four accesses: one at the point on the string where we want to pluck, one on the part of the pick which will touch the string, one on the part of the pick which we will move with our “hand,” and another at the point in the string where we will put our microphone (Modalys instruments, for the time being, can only be listened to using “contact microphones,” i.e., one can put one’s ear anywhere on the instrument, but not in the air).
Imagine, having specified the last bit of information about our instrument, that we send it off to the manufacturing department. It comes back as a large black box labeled “Plucked string instrument” with a speaker, and several knobs which correspond to all of the controllers which we specified (“constant” controllers can be thought of as knobs that are glued in one place). Hence we have built a basic instrument, and made some basic choices about how it is to be played. Now we are left with the task of actually making music with it. To play this particular instrument, we need to move the pick across the string so that the two objects make contact. This can be achieved by turning the knob that moves the large end of the pick (i.e., the part that one normally holds). The method by which the knob is turned depends on the type of Modalys controller we used to make the knob. There are controller types which can read MIDI data from a file, follow breakpoint envelopes, etc. (Modalys has an extremely powerful control system; we will look at some complex control setups later.) Once we have specified all the control information, we now have a complete Modalys synthesis: the instrument, the “instrumentalist,” and the “performance.” Let us look more closely at the specific components of a Modalys synthesis.
Connecting Modalys with various environments: Lisp, Max/MSP, Open Music and MatLab.
- Modalys
- Summary
- An Introduction to Modalys
- Objects
- Accesses
- Connections
- Controllers
- The Modalys Workspace
- Appendix
